Preface:

Going through the Carnegie Mellon University CS 15-458/858 course "Discrete Differential Geometry" for fun with some friends.

Youtube playlist is here

Discrete Differential Geometry Week 1

Discrete Geometry : part signal processing, part differential geometry Goal of course is to link the perspectives. Learn to think about shape.

1. Derivations
2. Implement

Differential Geometry:

• language for talking about local properties of shape
• the connection of these local properties to global properties of shape
  • "local-global" relations

DDG is finite. Yet it captures many fundamental ideas (e.g. genus).

Grand vision:

Translate Differential Geometry into language suitable for computation.

Common approach:

1. Write down equivalent defns in smooth setting.
2. Apply each smooth definition to an object in the discrete setting.
3. Determine which properties are captured by each resulting inequivalent discrete defn.

Often results in "no free lunch" scenario. No discrete defn captures all smooth properties.

example: Curvature

A parameterized curve is a map $\gamma : [0,L] \rightarrow \mathbb{R}^2$ e.g. $\gamma : [0,2 \pi) \rightarrow \mathbb{R}^2; s \mapsto (\cos(n), \sin(s))$

Unit Tangent

$T(s) := \frac{d}{ds}\gamma(s) / |\frac{d}{ds}\gamma(s)|$

If $|\frac{d}{ds}\gamma(s)| = 1$ then say $\gamma$ is arc-length parameterized for the circle, it is arc-length parameterized so $T= (-\sin(s), \cos(s))$

Normal to a curve:

Let $\mathscr{T}$ be a quarter turn ccw, then $N(s) := \mathscr{T}T(s)$

e.g $N(s) = (-\cos(s), \sin(s))$ for the circle. (The normals point inward. Choose a convention and stick to it.)

Curvature

Curvature is the rate of change of the tangent. $\kappa(s) := <N(s), \frac{d}{ds} T(s)> \ = <N(s), \frac{d^2}{ds^2} \gamma(s)>$

Key ideas:

1. The curvature is a second derivative.
2. The curvature is a signed quantity.

Discretization

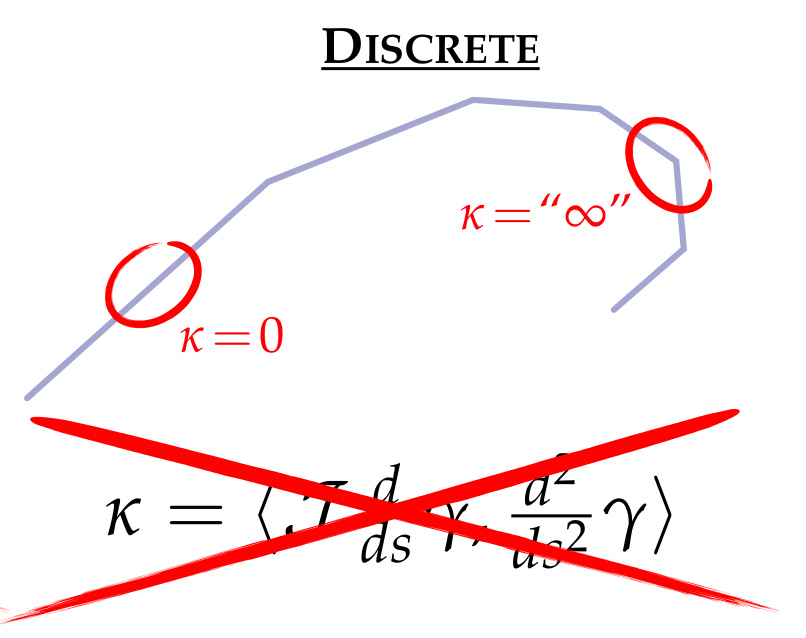
we only get either 0 or $\infty$.

We want it to have some properties like the smooth equivalent.

e.g.

1. Satisfies some properties which allow us to use theorems.
2. We can integrate it along the curve to reach the same result.
3. In the limit, the defn approaches the smooth curve.
4. Computational cost.

Other smooth definitions of curvature.

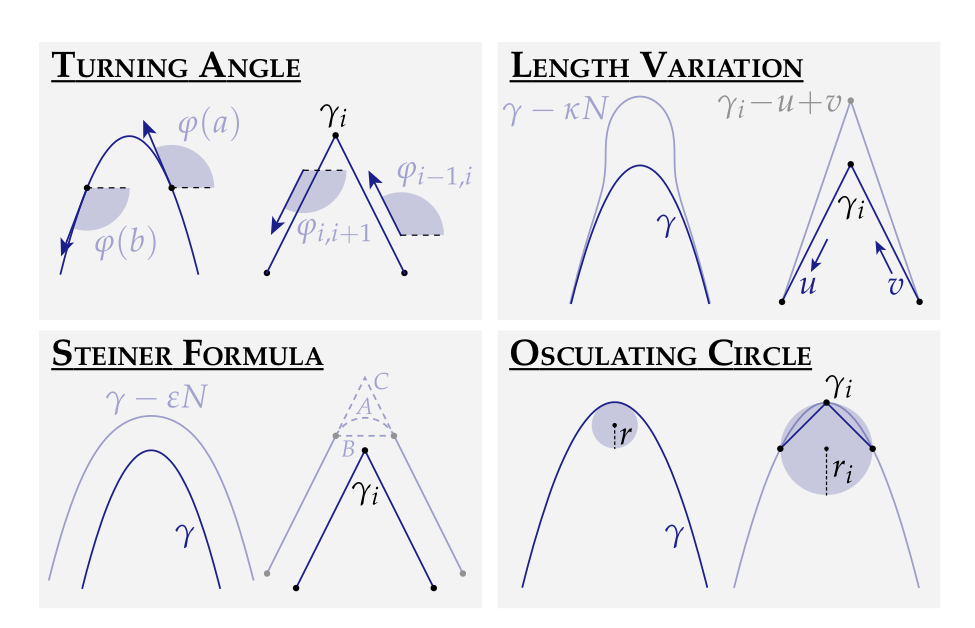
Can we apply some of these definitions to the discrete curve?

All four of these can be applied to the discrete case with different consequences.

Turning Angle

Equivalent to the first definition, we can measure the rate of change of the angle the tangent makes with the horizontal.

$\kappa(s) = \frac{d}{ds} \varphi(s)$

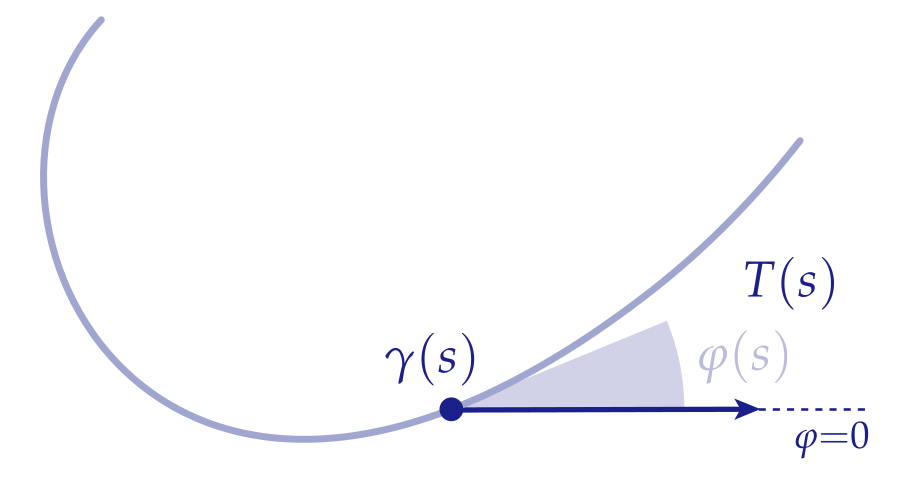
Still can't evaluate curvature of a discrete curve. The integral of curvature along a segment:

$\int_a^b \kappa(s) ds = \int_a^b \varphi(s)ds = \varphi(b) - \varphi(a)$

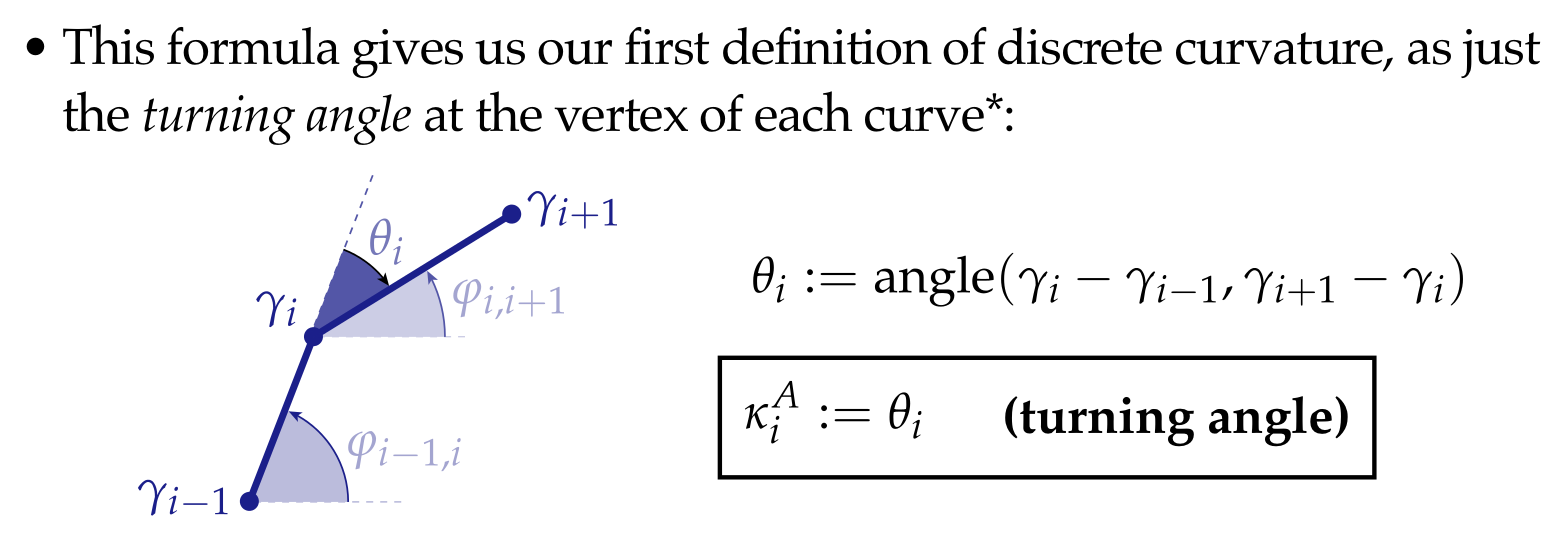
Most discrete quantities are integrated rather than pointwise quantities. e.g. total change in angle, rather than derivative of angle.

Length variation

Given this fact from the smooth setting:

The fastest way to decrease the length of a curve is to move it

in the normal direction, with speed proportional to curvature.

Displace curve by $\eta : [0,L] \rightarrow \mathbb{R}^2$ with $\eta(0)=\eta(L)=0$. (Perturbation)

Assignment

1. A Glimpse into Discrete Differential Geometry (pdf)

授業内容そのままっぽい

2. Architectural Geometry (pdf)

Helmut Pottmann, et al.

建築でZahaっぽいのを作るときにDDGが効いてくる話。主に4辺形Meshの作り方みたいなところにフォーカスしてたっぽい。前やってた多目的最適化みたいなところに帰ってきてほぎゃ～となった。確かにDesign Optimizationの論文とかは建築が多かったので進んでても驚きはないけど。

conjugate curve networkなる概念よくわからなかった（前提）調べてもGrasshopperの話しか出てこなかった。

3. DDG Consistency as Integrability

さっぱりわからなかった。連続的な微分幾何だと証明が難しかった可積分系の概念たちが離散化したら生えてきた、みたいな話っぽい？ 前提とされている両概念わからないので何もわからなかったけど数学って感じがした。

Darboux Transformってのが大事そう