DDG Week2 Writing Assignment

2.1

Show that $V - E + F = 1$ for any polygonal disk.

For a simple n-sided polygon with n vertices, n edges, and 1 face, the equation above holds. When conncting another n-sided polygon to form a disk, the polygon can connect to the existing disk by merging $m$ edges. This will generate $n-m$ edges, $n-(m+1)$ vertices, and 1 new face.

The last equality stems from our inductive assumption.

2.2

In a platonic solid, there are $F$ m, n-gons meeting at $V$ vertices.

$(F/m) - (nF/2) + F = 2$

2.8

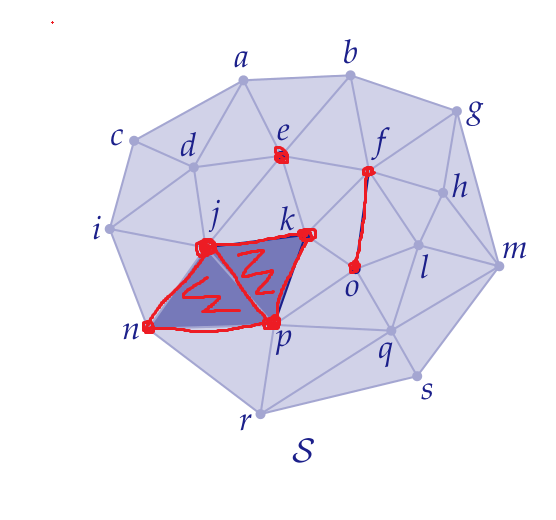
Cl(S)

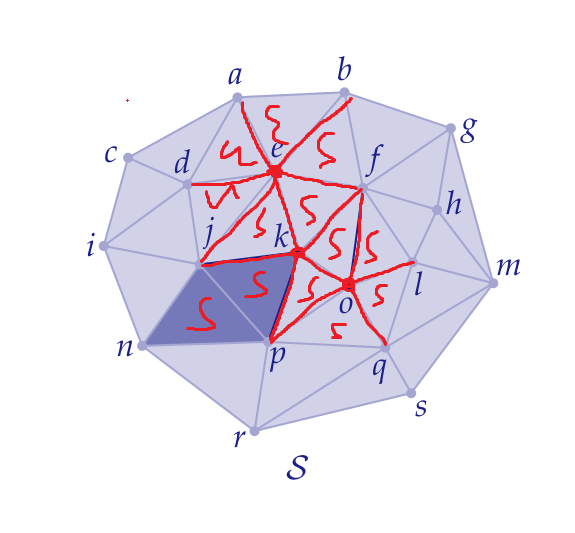
St(S)

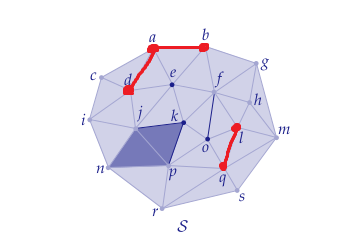
Lk(S)

2.9

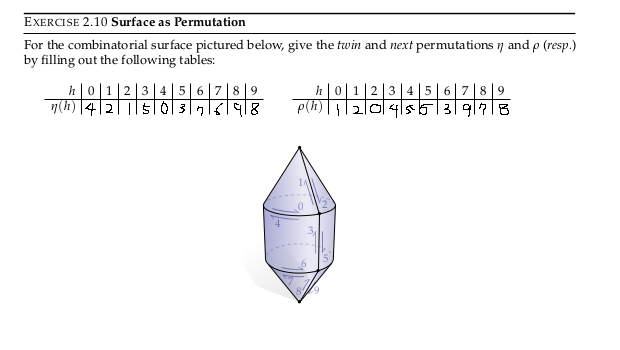
2.10

2.11

A0 = [
  [1,1,0,0,0],
  [1,0,1,0,0],
  [1,0,0,1,0],
  [1,0,0,0,1],
  [0,1,0,0,1],
  [0,1,1,0,0],
  [0,0,1,1,0],
  [0,0,0,1,1]
]

A1 = [
  [1,0,0,1,1,0,0,0],
  [1,1,0,0,0,1,0,0],
  [0,1,1,0,0,0,1,0],
  [0,0,1,1,0,0,0,1]
]

Coding

Code is somewhere, I haven't decided where to put it. The screenshots below should verify that the c++ code is working to solve the exercises.

All tests green:

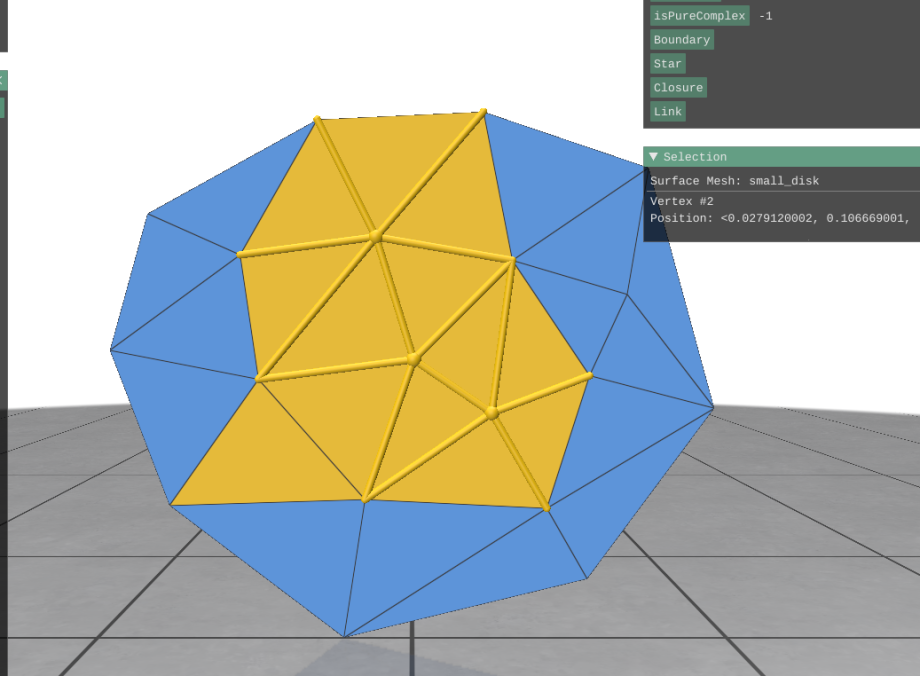
Star

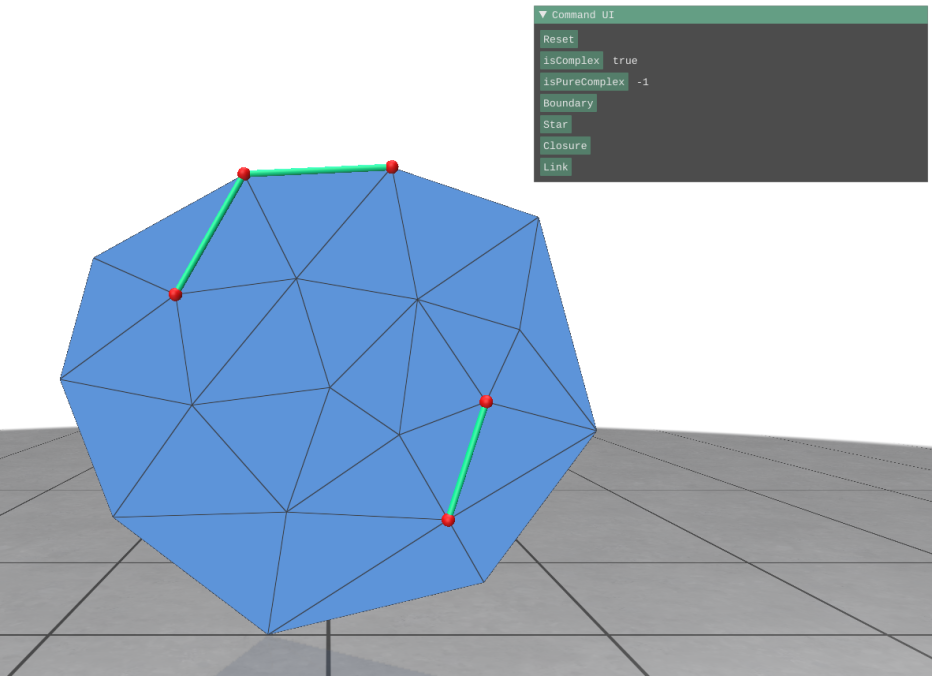
Link

Closure